Note. Vì mình cũng đang trong quá trình tìm hiểu về diffusion models nên tạm thời blog sẽ ngừng các bài viết trong chủ đề NLP lại một thời gian để tập trung cho diffusion models nhé 😀

Giới thiệu về diffusion models

Trong thời gian gần đây, xu hướng “AI vẽ tranh" đang rất là hot và các mô hình sinh ảnh nổi tiếng đó hầu hết là dựa trên diffusion models, đặc biệt là Stable Diffusion.

Minh họa ảnh sinh bởi Stable Diffusion
Nguồn: Stable Diffusion Online

Bài toán Image Generation, hay Image Synthesis, không phải là bài toán mới mà ta đã có khá nhiều họ mô hình được nghiên cứu và công bố. Cơ bản nhất là Autoencoder, Variational Autoencoder (VAE), Normalizing Flow và nổi tiếng nhất là Generative Adversarial Network. Trong image generation thì ta có một cái gọi là generative trilemma. Ý nghĩa của cái này là các mô hình sinh ảnh sẽ chỉ đạt được nhiều nhất là 2 trong 3 tiêu chí sau: Thời gian sinh ảnh nhanh, chất lượng ảnh rõ nét và nội dung ảnh đa dạng.

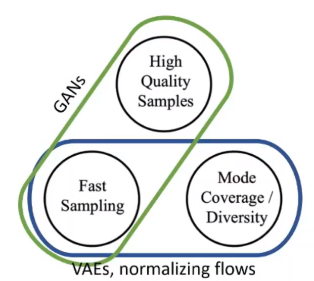
The generative trilemma
Nguồn: Tanishq Abraham

• GAN thì sinh ảnh nhanh và chất lượng ảnh rõ nét nhưng các ảnh nó sinh ra thường trông khá giống nhau, tức là thiếu sự đa dạng
• VAE và Normalizing Flow thì đạt được mặt tốc độ và đa dạng nhưng chất lượng ảnh thì không tốt lắm.

Với diffusion models, ta thường đạt được tiêu chí chất lượng và sự đa dạng nhưng tốc độ thì lại khá chậm. Do đó, hầu hết các cải tiến trong difusion models là liên quan đến việc tăng tốc quá trình sinh ảnh.

Ý tưởng chung của diffusion models là ta từng bước thêm nhiễu vào ảnh ban đầu để “phá hủy” phân phối của dữ liệu, sau đó học cách khôi phục lại cấu trúc của ảnh gốc. Sau đó, để sinh ảnh thì ta xuất phát từ một ảnh nhiễu hoàn toàn và từ từ khử nhiễu để có được ảnh kết quả.

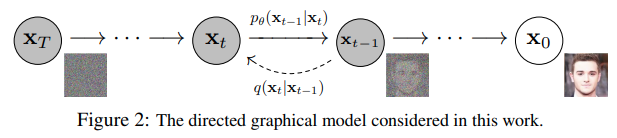
Ý tưởng chung của diffusion models

Mô hình Diffusion Probability Model được giới thiệu đầu tiên trong paper năm 2015 là Deep Unsupervised Learning using Nonequilibrium Thermodynamics. Phần toán của mô hình này rất là nặng và nó ít được cộng đồng để ý tới khi mà kết quả lúc được công bố thì cũng không có gì nổi bật. Mãi đến năm 2020, Denoising Diffusion Probability Model (DDPM) được công bố và có thể nói đây là sự kiện quan trọng khi nhờ paper này mà diffusion models mới trở thành một chủ đề nghiên cứu được nhiều người quan tâm.

Nói đến các mô hình ảo diệu như Stable Diffusion thì ta còn có nhiều chi tiết khác nữa nhưng nó sẽ không nằm trong phạm vi bài viết này. Mình sẽ tập trung vào phần lý thuyết toán của mô hình để làm nền tảng cho các bài viết sau.

Forward diffusion

Giả sử data sample (“ảnh” ban đầu) được lấy mẫu từ phân phối dữ liệu thật sự $\bold{x}_0 \sim q(\bold{x})$. Feed forward là quá trình ta thêm một lượng nhỏ Gaussian noise vào data sample $\bold{x}_0$ thông qua $T$ bước, từ đó có các noisy samples $\bold{x}_1, \bold{x}_2,…, \bold{x}_T$. Phân bố của data sample $\bold{x}_t$ chỉ phụ thuộc vào $\bold{x}_{t-1}$ như sau:

$$ \begin{equation} q(\bold{x}_t | \bold{x}_{t-1}) = \mathcal{N}\left(\bold{x}_{t-1}; \sqrt{1-\beta_t} \bold{x}_{t-1}, \beta_t \bold{I} \right) \end{equation} $$

Công thức $(1)$ có nghĩa là “ảnh” tại bước thứ $t$ được sample từ một conditional Gaussian distribution với mean $\mu_t = \sqrt{1 - \beta_t} \bold{x}_{t-1}$ và variance $\sigma^2 = \beta_t$. Với giả thiết sự phụ thuộc, ta cũng có thể xem đây là một xích Markov.

• Lưu ý. $q$ là probability density fuction (hàm mật độ xác suất) của phân phối chuẩn.

Minh họa quá trình forward
Nguồn: Steins

Bằng re-parameterization trick, ta có thể sample $\bold{x}_t$ như sau:

$$ \begin{equation} \bold{x}_t = \sqrt{1 - \beta_t} \bold{x}_{t-1} + \epsilon_{t-1} \sqrt {\beta_t} \end{equation} $$

với $\epsilon_{t-1} \sim \mathcal{N}(\bold{0}, \bold{I})$.

Các giá trị phương sai $\beta_t$ là được định nghĩa trước và nó được gọi là variance scheduler. Ta sẽ đề cập kĩ hơn về scheduler ở phần 4. Trước hết thì có một số nhận xét như sau:

• $0 < \beta_1 < \beta_2 < … < \beta_T < 1$
• Có thể hiểu rằng càng đến các bước sau thì ta thêm càng nhiều nhiễu vào data sample (vì variance ngày càng lớn). Khi $t \to \infty$, phân bố của $\bold{x}_T$ sẽ tương đương với isotropic Gaussian distribution, tức là $\bold{x}_T \sim \mathcal{N}(\bold{0}, \bold{I})$.

Quay trở lại với công thức xác định phân phối của $\bold{x}_t$. Để xác định phân phối của $\bold{x}_T$ thì ta sẽ tính dần từng bước như sau:

$$ \begin{equation} q(\bold{x}_{1:T} \vert \mathbf{x}_0) = \prod^T_{t=1} q(\bold{x}_t \vert \bold{x}_{t-1}) \end{equation} $$

Tính như trên thì trông có vẻ là khá lâu!

Một tính chất thú vị của quá trình forward là ta có thể sample được ngay $\bold{x}_t$ với bất kì timestep $t$ nào. Đặt $\alpha_t = 1 - \beta_t$ và $\bar{\alpha}_t = \prod_{i=1}^t \alpha_i$. Vì $\beta_t$ đều được xác định sẵn nên ta cũng sẽ tính trước được $\bar{\alpha_t}$. Từ công thức $(2)$ ta có

$$ \begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1} \\ &= \sqrt{\alpha_t \alpha_{t-1}} \bold{x}_{t-2} + \sqrt{\alpha_t - \alpha_t \alpha_{t-1}} \epsilon_{t-2} + \sqrt{1 - \alpha_t} \epsilon_{t-1} \end{aligned} $$

Khi ta gộp hai Gaussion distribution $\mathcal{N}(\bold{0}, \sigma_1^2 \bold{I})$ và $\mathcal{N}(\bold{0}, \sigma_2^2 \bold{I})$ (ý nói đến hai đại lượng chứa $\epsilon_{t-2}$ và $\epsilon_{t-1}$ ở trên) thì phân phối thu được sẽ là $\mathcal{N}(\bold{0}, (\sigma_1^2 + \sigma_2^2) \bold{I})$. Do đó, từ công thức trên ta có thể viết lại thành

$$ \mathbf{x}_t = \sqrt{\alpha_t \alpha_{t-1}} \bold{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\epsilon}_{t-2} $$

Cứ tiếp tục biến đổi thì ta sẽ có

$$ \mathbf{x}_t = \sqrt{\bar{\alpha_t}} \bold{x}_{0} + \sqrt{1 - \bar{\alpha_t}} \epsilon $$

với $\epsilon \sim \mathcal{N}(\bold{0}, \bold{I})$.

Tóm lại, trong quá trình forward, ta có thể sample $\bold{x}_t$ dựa vào phân phối sau:

$$ q(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) $$

Reverse diffusion

Đặt vấn đề

Quá trình forward diffusion dần dần thêm các Gaussian noise vào sample dựa theo các phân phối $q(\bold{x}_t|\bold{x}_{t-1})$. Nếu ta có thể đi ngược lại, tức là xuất phát từ một sample $\bold{x}_{T} \sim q(\bold{x}_T) = \mathcal{N}(\bold{0}, \bold{I})$ và dần sample $\bold{x}_{t-1}$ theo phân phối $q(\bold{x}_{t-1} | \bold{x}_t)$ nào đó thì khi thực hiện cho đến $\bold{x}_0$, ta đã có thể denoise (khử nhiễu) để thu lại được sample xấp xỉ sample ban đầu của quá trình forward.

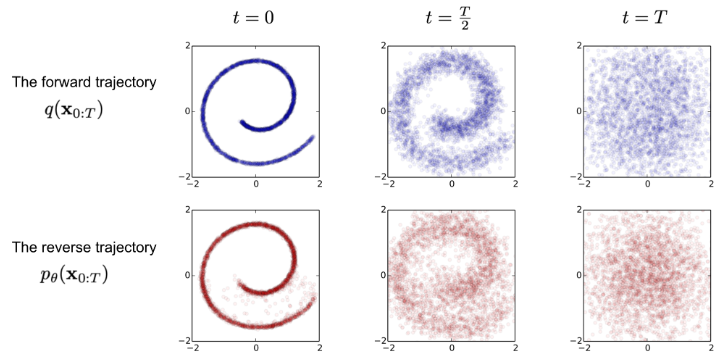
Minh họa quá trình forward và reverse

Tuy nhiên, việc xác định $q(\bold{x}_{t-1} | \bold{x}_t)$ là rất khó vì nó liên quan đến phân phối của toàn bộ dữ liệu. Do đó, ta sẽ tìm cách xấp xỉ phân phối này.

• Kĩ hơn về lý do khó xác định $q(\bold{x}_{t-1} | \bold{x}_t)$: Vì có rất nhiều khả năng có thể xảy ra đối với $\bold{x}_{t-1}$ nên phương sai của phân phối này cũng sẽ rất lớn.
• Giả sử ta cần xác định $q(\bold{x}_{t-1} | \bold{x}_t, \bold{x}_0)$ thì mọi chuyện sẽ dễ dàng hơn. Khi biết trước thêm $\bold{x}_0$ nữa thì ta có thể hình dung được $\bold{x}_{t-1}$ nên trông như thế nào. Kĩ thuật này gọi là variance reduction step.
• Một cách trực giác, ta đoán được những gì cần làm khi biết thêm $\bold{x}_0$ là thực hiện nội suy $\bold{x}_{t-1}$ dựa vào $\bold{x}_0$ và $\bold{x}_{t}$. Ta sẽ quay lại với nhận xét này sau.

Để ý rằng với $\bold{x}_T \sim \mathcal{N}(\bold{0}, \bold{I})$ và $\beta_T$ đủ nhỏ thì $q(\bold{x}_{T-1}|\bold{x}_T)$ cũng là một Gaussian distribution. Một cách đệ quy, ta có thể xem toàn bộ $q(\bold{x}_{t-1} | \bold{x}_t)$ là Gaussian distribution luôn 😀 Để xấp xỉ $q(\bold{x}_{t-1} | \bold{x}_t)$, ta sẽ sử dụng một mô hình $p_{\theta}$ để dự đoán giá trị mean $\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)$ và variance $\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)$. Từ đó xấp xỉ được

$$ p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) $$

• Lưu ý rằng các giá trị đầu vào của mô hình bao gồm cả $\bold{x}_t$ và timestep $t$ (cho biết mức độ noise được dùng để tạo ra $\bold{x}_t$ trong quá trình forward).
• Mô hình $p_\theta$ thường là U-Net. Tạm thời ta sẽ bỏ qua chi tiết về kiến trúc của mô hình này.

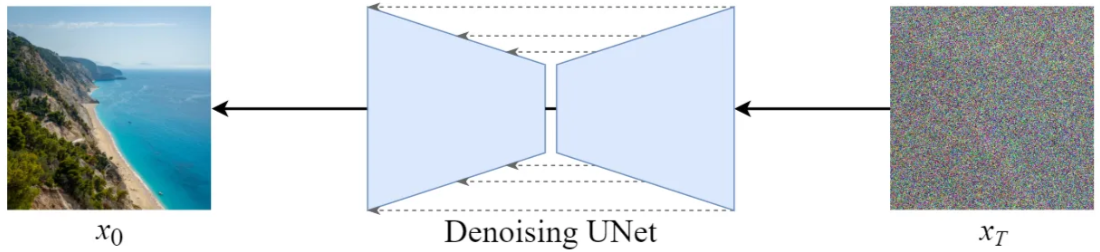
Minh họa mô hình U-Net trong quá trình reverse
Nguồn: Steins

• Trong quá trình forward, ta đã đề cập là các giá trị variance đã được xác định trước dựa vào scheluder nên ở đây thì ta không cần dự đoán variance. Khi đó

$$ p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \beta_t \bold{I}) $$

Giả sử ta đã học được mô hình $p_{\theta}$ như trên thì từ $\bold{x}_T$ ta có thể xấp xỉ được phân phối của $\bold{x}_0$ như sau:

$$ p_\theta (\bold{x}_{0:T}) = q (\bold{x}_T) \prod_{t=1}^T p_\theta (\bold{x}_{t-1} | \bold{x}_t) $$

Vấn đề đặt ra là ta huấn luyện mô hình $p_\theta$ như thế nào. Vậy thì ta cần phải tìm loss function!

Xác định loss function

Mục tiêu của ta là minimize the negative log likelihood $-\log p_\theta (\bold{x}_0)$. Biến đổi một chút như sau:

$$ \begin{aligned} -\log p_\theta(\mathbf{x}_0) &\leq - \log p_\theta(\mathbf{x}_0) + D_\text{KL}(q(\mathbf{x}_{1:T}\vert\mathbf{x}_0) \| \color{red}p_\theta(\mathbf{x}_{1:T}\vert\mathbf{x}_0) \color{default} ) \\ &= -\log p_\theta(\mathbf{x}_0) + \mathbb{E}_{\mathbf{x}_{1:T}\sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{\color{red}p_\theta(\mathbf{x}_{0:T}) / p_\theta(\mathbf{x}_0)} \Big] \\ &= -\log p_\theta(\mathbf{x}_0) + \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} + \log p_\theta(\mathbf{x}_0) \Big] \\ &= \mathbb{E}_q \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \end{aligned} $$

Đặt $L_{VLB} = \mathbb{E}_q \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big]$ (variational lower bound). Nhận xét rằng nếu minimize được $L_{VLB}$ thì giá trị của negative log likelihood cũng sẽ nhỏ 😀 Do đó, hàm mục tiêu của ta sẽ là $L_{VLB}$.

Tiếp tục biến đổi $L_{VLB}$, ta có

$$ \begin{aligned} L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log\frac{\color{red}q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{\color{blue}p_\theta(\mathbf{x}_{0:T})} \Big] \\ &= \mathbb{E}_q \Big[ \log\frac{\color{red}\prod_{t=1}^T q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{\color{blue} p_\theta(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) } \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=1}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{\color{green}q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \Big( \frac{\color{green}q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)}\cdot \frac{\color{green}q(\mathbf{x}_t \vert \mathbf{x}_0)}{\color{green}q(\mathbf{x}_{t-1}\vert\mathbf{x}_0)} \Big) + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \end{aligned} $$

• Trong dòng biến đổi ở trên, áp dụng công thức Bayes thì ta có

  $$ q(\bold{x}_t | \bold{x}_{t-1}) = \frac{q(\bold{x}_{t-1} | \bold{x}_t) \cdot q(\bold{x}_t)}{q(\bold{x}_{t-1})} $$

  Ta có nhận xét ảo ma rằng nếu ta cho thêm một điều kiện là $\bold{x}_0$ thì các giá trị trên sẽ dễ tính hơn rất nhiều (có thể tận dụng quá trình forward). Vậy thì “assume” luôn là

  $$ q(\bold{x}_t | \bold{x}_{t-1}) = \frac{q(\bold{x}_{t-1} | \bold{x}_t, \bold{x}_0) \cdot q(\bold{x}_t | \bold{x}_0)}{q(\bold{x}_{t-1} | \bold{x}_0)} $$

OK, tiếp tục biến đổi $L_{VLB}$:

$$ \begin{aligned} L_\text{VLB} &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \color{red}\sum_{t=2}^T \log \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1} \vert \mathbf{x}_0)} \color{default} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \color{red}\log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{q(\mathbf{x}_1 \vert \mathbf{x}_0)} \color{default} + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big]\\ &= \mathbb{E}_q \Big[ \color{green}-\log p_\theta(\mathbf{x}_T) \color{default} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{\color{green}q(\mathbf{x}_T \vert \mathbf{x}_0)}{\color{blue}p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \\ &= \mathbb{E}_q \Big[ \color{green}\log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_T)} \color{default} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} - \color{blue}\log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)\color{default} \Big] \end{aligned} $$

Và bước cuối cùng:

$$ \begin{aligned}L_{LVB} &= \mathbb{E}_q [\color{red}\underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} \color{default} + \color{blue}\sum_{t=2}^T \underbrace{D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))}_{L_{t-1}} \color{green} \underbrace{- \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} ] \\ &= L_T + \left (L_1 + L_2 + \cdots + L_{T-1}\right) + L_0 \end{aligned} $$

• Nhìn chung thì đây toàn là loss liên quan đến khoảng cách các phân phối trong từng timestep.

Vì $\bold{x}_T \sim \mathcal{N}(\bold{0}, \bold{I})$ nên $L_T$ là một hằng số (khi $T \to \infty$ thì $L_T \to 0$) và ta có thể bỏ qua nó. Ngoài ra, vì giá trị phương sai $\beta_1$ là rất nhỏ và thường thì “ảnh" $\bold{x}_0$ và $\bold{x}_1$ trông sẽ rất giống nhau (vì lượng nhiễu thêm vào là rất ít). Vì lý do này mà các tác giả của DDPM thật sự đã bỏ qua nó trong quá trình huấn luyện.

Như vậy ta còn lại mỗi $L_t$ với $1 \leq t \leq T - 1$. Đối với cái này thì cần có một số ma thuật.

Tham số hóa $L_t$

Các giá trị $L_t$ với $1 \leq t \leq T - 1$ liên quan đến khoảng cách giữa phân phối được xấp xỉ bởi model $p_\theta$ và một phiên bản “dễ tính hơn” của $q(\bold{x}_{t-1} | \bold{x}_t)$ là $q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)$ . Ta sẽ đi tính mean và variance của phân phối này.

Đầu tiên, áp dụng quy tắc Bayes thì

$$ q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0)} $$

Cả 3 phân phối trên đều là Gaussian distribution trong quá trình forward và ta đã biết được mean, variance của chúng. Nhắc lại một chút: Công thức hàm mật độ xác suất của Gaussian distribution $\cal{N}(\mu,\sigma)$ là

$$ f(x) = \frac{1}{\sigma \sqrt{2 \pi}} \exp \left( -\frac{1}{2} \left( \frac{x - \mu}{\sigma} \right)^2\right) $$

Do đó

$$ \begin{aligned} q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &\propto \exp \left(-\frac{1}{2} \left(\frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \right) \right) \\ &= \exp \left(-\frac{1}{2} \left(\frac{\mathbf{x}_t^2 - 2\sqrt{\alpha_t} \mathbf{x}_t \color{blue}{\mathbf{x}_{t-1}} \color{default}{+ \alpha_t} \color{red}{\mathbf{x}_{t-1}^2} }{\beta_t} + \frac{ \color{red}{\mathbf{x}_{t-1}^2} \color{default}{- 2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0} \color{blue}{\mathbf{x}_{t-1}} \color{default}{+ \bar{\alpha}_{t-1} \mathbf{x}_0^2} }{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \right) \right) \\ &= \exp \left( -\frac{1}{2} \left( \left( \frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}} \right) \color{red} \bold{x}_{t-1}^2 \color{default} - \left( \frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2 \sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \bold{x}_0 \right) \color{blue}\bold{x}_{t-1} \color{default} + C(\bold{x}_t, \bold{x}_0)\right)\right)\\ \end{aligned} $$

với $C(\bold{x}_t, \bold{x}_0)$ là những đại lượng không liên quan đến $\bold{x}_{t-1}$ và có thể được bỏ qua.

Ta cần biến đổi công thức trên về dạng của một Gaussian distribution. Đặt

$$ \tilde{\beta}_t = 1/\left(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}\right) = 1/\left(\frac{\alpha_t - \bar{\alpha}_t + \beta_t}{\beta_t(1 - \bar{\alpha}_{t-1})}\right) = {\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} $$

và

$$ \begin{aligned} \tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \bold{x}_0) &= \left(\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0\right)/\left(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}\right) \\ &= \left(\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0\right) {\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\ &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\color{green}\beta_t}{1 - \bar{\alpha}_t} \color{red}\mathbf{x}_0 \end{aligned} $$

Từ quá trình forward, ta có thể suy ra rằng $\bold{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon})$ với $\boldsymbol{\epsilon} \sim \cal{N}(\bold{0}, \bold{I})$. Do đó

$$ \begin{aligned} \tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, t) &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\color{green}(1 - \alpha_t)}{1 - \bar{\alpha}_t} \color{red}\frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}) \\ &= \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon} \right) \end{aligned} $$

Khi đó ta có

$$ q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \propto \exp \left( -\frac{1}{2} \frac{\left( \bold{x}_{t-1} - \tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, t) \right)^2}{\tilde{\beta}_t} \right) $$

, tức là

$$ q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \cal{N}(\bold{x}_{t-1};\tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, t), \tilde{\beta}_t\bold{I}) $$

Mặt khác, trong phần đặt vấn đề của quá trình reverse thì ta cần huấn luyện mô hình $p_\theta$ để dự đoán giá trị mean $\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)$, sao cho

$$ p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \beta_t \bold{I}) $$

Điều này nghĩa là thứ ta cần quan tâm về $\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)$ là dự đoán được $\tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, t)$, mà cụ thể hơn là dự đoán giá trị $\epsilon \sim \cal{N}(\bold{0}, \bold{I})$ (vì toàn bộ những giá trị khác trong $\tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, t)$ đều đã biết vì chúng là input của quá trình reverse). Từ đó, ta có thể biểu diễn

$$ \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) = {\frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \color{red}\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \color{default} \right)} $$

• Dự đoán $\epsilon_t$ cũng có nghĩa là đi dự đoán lượng nhiễu được thêm vào $\bold{x}_{t-1}$ để tạo ra $\bold{x}_{t}$ trong quá trình forward trước đó.

Như vậy, thành phần loss $L_{t-1}$ sẽ trở thành

$$ \begin{aligned} L_{t-1} &= D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)) \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \| \beta_t \bold{I} \|^2_2} \| \color{blue}{\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - \color{green}{\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \color{default} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \|\beta_t \bold{I} \|^2_2} \| \color{blue}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon} \Big)} - \color{green}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) \Big)} \color{default}\|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \beta_t \bold{I} \|^2_2} \|\boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \end{aligned} $$

Các tác giả của DDPM cho rằng lược bỏ phần trọng số sẽ giúp mô hình học tốt hơn. Khi đó ta có phiên bản đơn giản hơn của $L_{t-1}$ là

$$ \begin{aligned} L_{t-1}^\text{simple} &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\|\boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\|\boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}, t)\|^2 \Big] \end{aligned} $$

, hay diễn tả dễ hiểu hơn thì đây là Mean Squared Error giữa lượng nhiễu dự đoán và lượng nhiễu thật sự.

Variance scheduler

Trong các phần trước, ta có đề cập đến việc các giá trị variance $\beta_t$ là cố định và chúng được xác định trước bằng cách sử dụng variance chueduler.

Vì sao cần dùng đến scheduler?

• Việc sử dụng schedule làm cho quá trình forward của diffusion model là cố định và có thể xác định trước. Điều này có thể giúp cho các tính toán của quá trình reverse trở nên gọn nhẹ hơn mà không làm ảnh hưởng gì đến độ hiệu quả của mô hình.

Có nhiều dạng schedule khác nhau như linear, cosine. Trong paper DDPM 2020 thì các tác giả sử dụng linear variance scheduler với $\beta_1 = 10^{-4}$ và $\beta_T = 0.02$.

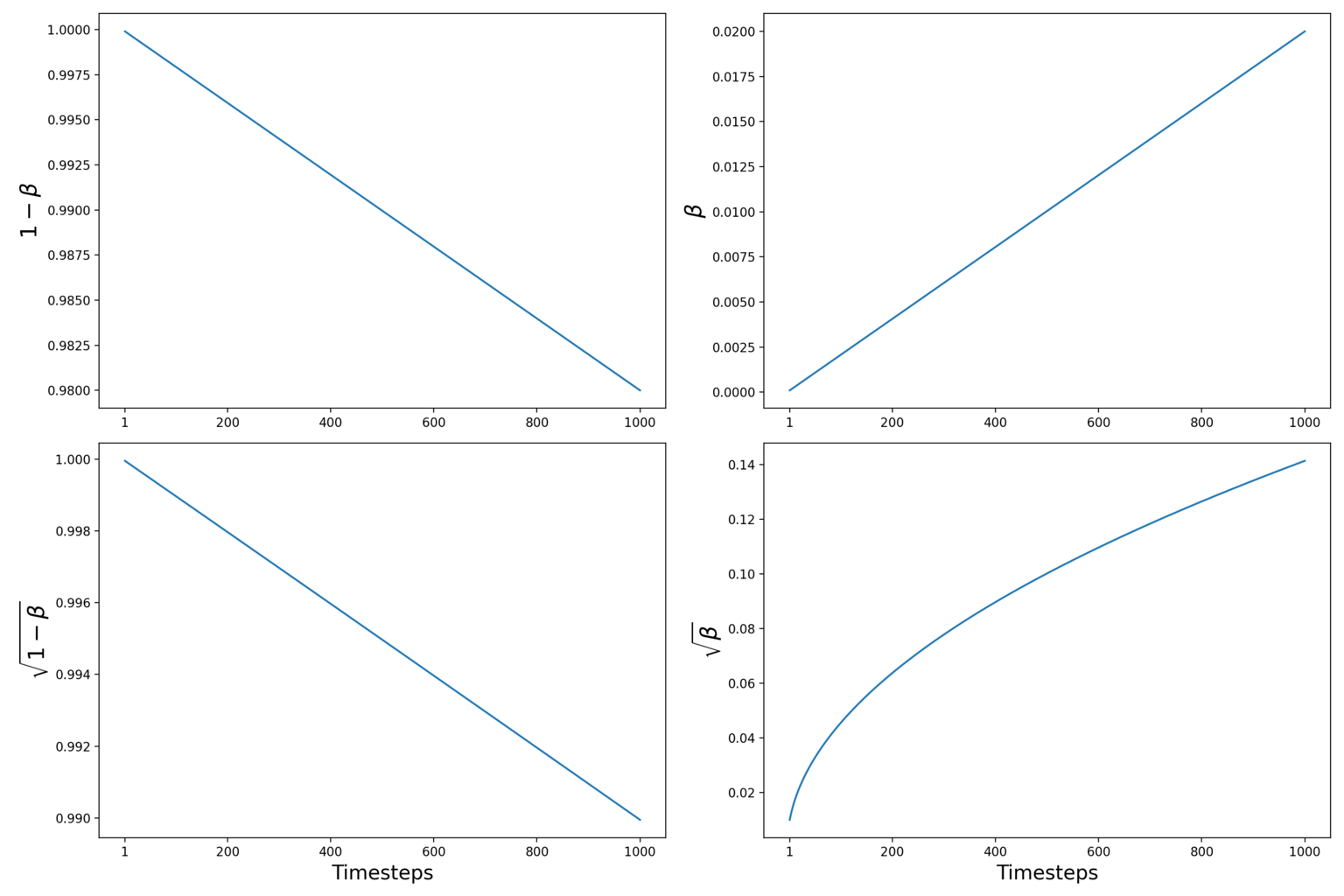
Minh họa cho linear variance scheduler

Trong paper Improved Denoising Diffusion Probabilistic Models - 2021, người ta cho rằng sử dụng cosine variance scheduler sẽ mang lại kết quả tốt hơn. Vấn đề chủ yếu nằm ở chỗ với linear thì ở những timesteps phía sau thì hầu như ảnh đã trở thành “isotropic Gaussian distribution” (có vẻ ý là linear thì thêm nhiễu hơi bị nhanh). Ở hình bên dưới thì hàng trên là linear, hàng dưới là cosine.

Linear scheduler và Cosine scheduler

Quá trình training và sampling

Dù các nền tảng lý thuyết bên dưới của diffusion model trông rất rối nhưng quá trình training và sampling (inference) thì rất đơn giản.

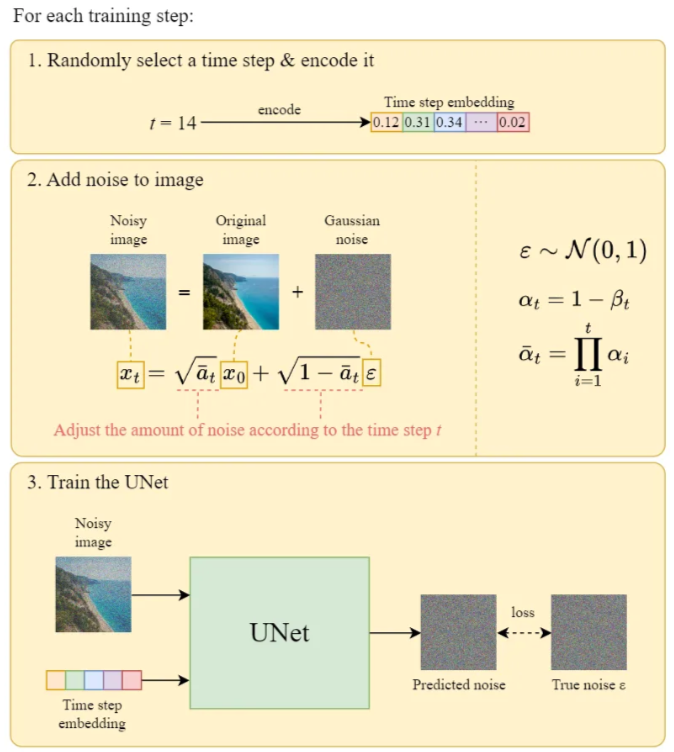
Đầu tiên, ta xét quá trình training:

• Ta cần train mô hình dự đoán nhiễu.
• Có một chi tiết là các tác giả của paper DDPM cho rằng việc training sẽ hiệu quả hơn khi ta chọn ngẫu nhiên các timestep $t$ và chỉ dự đoán nhiễu tại timestep đó, thay vì phải dự đoán ở toàn bộ timestep như những gì được biểu diễn trong hàm loss ở phần 3.2.

Mã giả cho quá trình training

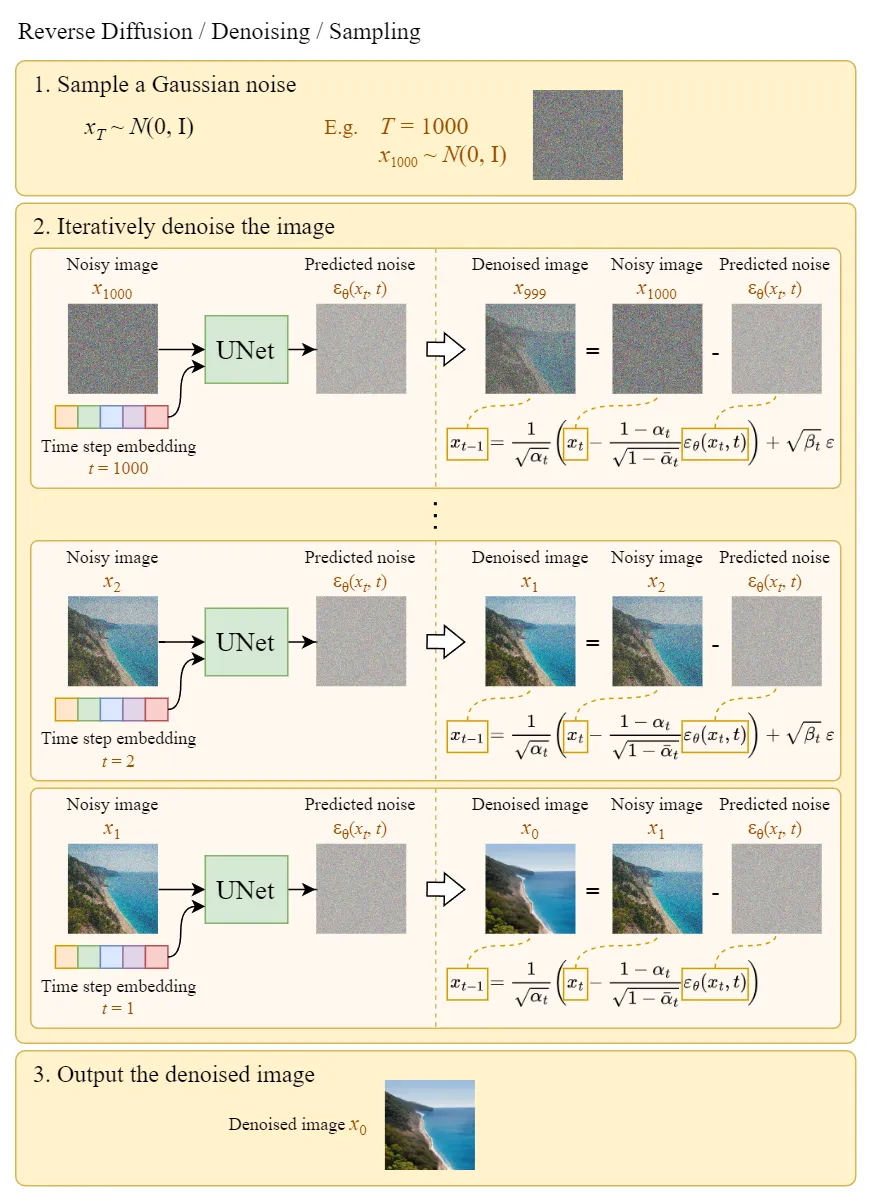
Trong quá trình sampling (inference) thì ta sẽ chọn trước số lượng timestep tối đa $T$. Bắt đầu từ $\bold{x}_T \sim \cal{N}(\bold{0}, \bold{I})$. Từ đó, dần qua các bước reverse thì:

• Dự đoán nhiễu $\epsilon_\theta(\bold{x}_t, t)$.
• Sample $\bold{x}_{t-1}$ với bằng re-parameterization trick

Mã giả cho quá trình sampling

• Lưu ý. Trong mã giả của quá trình sampling, khi sampling $\bold{x}_0$ thì ta không thêm nhiễu. Điều này khớp với chi tiết bỏ qua thành phần loss $L_0$ ở trên :D

Minh họa trực quan cho quá trình training và sampling:

Nhận xét

Chỉ với những chi tiết trên thì có thể nói rằng diffusion models chưa thể vượt mặt GAN được về tốc độ sampling cũng như chất lượng ảnh. Ta vẫn còn nhiều cải tiến cho difusion models và những cải tiến này đã cùng nhau đưa diffusion models lên cạnh tranh vị trí top 1 trong bài toán Image Generation, trong đó nổi bật là sự xuất hiện của Stable Diffusion với những ma thuật như text-to-image, image-to-image và hơn thế nữa!.

Ta sẽ đề cập đến chúng trong các bài viết sau.

Tài liệu tham khảo

• Jascha Sohl-Dickstein et al. “Deep Unsupervised Learning using Nonequilibrium Thermodynamics.” ICML 2015.
• Jonathan Ho et al. “Denoising diffusion probabilistic models.” arxiv Preprint arxiv:2006.11239 (2020).
• Lilian Wenge, What are diffusion models?
• The AI Summer, Diffusion models
• HuggingFace’s Blog, Annotated Diffusion
• Steins, Diffusion Model Clearly Explained!
• Outlier, Diffusion Models | Paper Explanation | Math Explained
• Tanishq Abraham, Diffusions Study Group